RC 直列回路と直流電圧源

ここでは抵抗 (Register) とコンデンサ (Capacitor) が、乾電池などの直流電圧源に直列に接続されている場合について考えてみましょう。

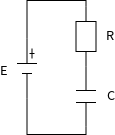
抵抗 (R) とコンデンサ (C) で構成されているので RC 回路と呼びます。

【まとめ】

コンデンサに蓄えられる電荷は静電容量かける電圧。

\[q = C \cdot v_c \]

電流の流れは電荷の時間変化 (\(t\) で微分)

\[ i = \frac{dq}{dt} = C \frac{dv_c}{dt} \]

コンデンサの電圧は次の式で上昇。

\[ v_c(t) = E \Big( 1- e^{- \frac{1}{RC} t} \Big) \]

これは微分方定式を変数分離法かラプラス変換とかで解くと出てくる。

時定数 \(\tau = RC\) 時間でおよそ 63% 充電。\(5\tau\) 時間でほぼフル充電。

RC 回路で何が起きる？電流は流れる？

こんな風に接続すると、一体何が起きるでしょうか。

ボタンのスイッチを取り付けて、ボタンを押したときだけ電池が繋がる状態にします。そして、スイッチを押す前は、コンデンサの中には電荷が空っぽの状態とします。

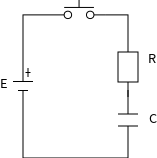
では、ボタンを押して電池を接続してみましょう。

すると、ボタンを押した直後に、コンデンサには電荷が蓄えられていきます。いっぱいに電荷が溜まるとそれ以上は電荷を蓄えられなくなります。

「電荷の流れ」= 「電流」です。つまり、コンデンサに電荷がいっぱいに溜まるまでは回路に電流が流れるけど、コンデンサに電荷がいっぱいになると電流の流れが止まる、ということです。

電流が止まったら、コンデンサの両端の電圧差は電源の \(E\) [V] になります。抵抗での電圧降下はオームの法則から、 \(V = IR\) ですが、電流が流れていないので \(I=0\) ですから \(V=0 \cdot R=0\) [V] です。

いつ何がどのくらいの量になる？

スイッチを押して電池をつないだら、はじめは電流は流れるけど、コンデンサに電荷がたまったら流れなくなることはわかりました。

でも、「はじめは」といっても実際は どのくらいの時間なのでしょうか？ 1 秒でしょうか？1時間でしょうか？もう少し正確に把握したいところです。

さらに、コンデンサの両端の電圧は最終的に電源と同じ \(E\) [V] になるわけですが、それはどのように変化していくのでしょうか？

よく考えると、まだわからないことが多いですね。もう少し詳しくみてみましょう。

コンデンサに蓄えられている電荷 \(q\) は、コンデンサの静電容量 \(C\) とコンデンサの両端での電圧 \(v_c\) の積になります。

\[ q = C \cdot v_c \]

時間で変わる量を小文字で、定数を大文字でかきます。

電荷 \(q\) の単位はクーロン、静電容量 \(C\) の単位はファラドといいます。

静電容量 \(C\) はコンデンサを構成する導体の面積や誘電体の種類などで決まります。このため、それぞれのコンデンサ毎に決まる定数になります。

コップに例えると、コップに入る水の量 (容積) がコップの形状や大きさで決まっているのと同じで、コンデンサもモノが決まれば容量 (静電容量) 決まります。

上で説明したように、電源を接続して十分長い時間が経過したあとは、コンデンサ両端の電圧 \(v_c\) は電池の電圧 \(E\) と等しくなって、これが電圧の最大値です。従って、蓄えられる電荷の最大量 \(q_{max}\) は電圧が最大になったときなので、 \(q_{max} = C \cdot E\) になります。

さて、キルヒホッフの電圧則というのがあって、回路をグルッと一回りしてくると電圧が上がったり下がったりして、それぞれの要素での電圧を足し合わせると 0 になります。

キルヒホッフの電圧則は省略形で KLV と省略します。

今回の場合は、電源で \(E\) [V] 上がって、抵抗で \(iR\) [V] 下がって、コンデンサで \(v_c\) 下がるとすると、次のように書けます。

\[ E - iR - v_c = 0 \]

コンデンサに蓄えられる電荷は \(q = C \cdot v_c\) で、「電荷の時間変化」がすなわち電流 \(i\) です。電流 \(i\) は \(q\) を時間 \(t\) で微分することで求められます。これらのことから、電流 \(i\) はコンデンサの電圧 \(v_c\) を使って、次のように書けます。

\[ \begin{aligned} i &= \frac{dq}{dt} \\ &= C \frac{dv_c}{dt} \end{aligned} \]

これを上の式に代入すると、次の式が得られます。

\[ E - RC \frac{dv_c}{dt} - v_c = 0 \]

この微分方定式を解くことで \(v_c\) がどうなるかわかるはずですね。

微分方定式を解く

この微分方定式を解くのは高校数学位の話なので、簡単に解けるよ、という人は計算過程はスッ飛ばして結論をみてください。

ここでは数学の復習兼ねて計算過程も載せておきます。変数分離法で解く方法とラプラス変換を使った方法の二通り記載します。

上記の微分法定式を解けば次のようになります。

\[ v_c(t) = E \Big( 1- e^{- \frac{1}{RC} t} \Big) \]

これで \(v_c\) がわかりました。

グラフを描く

\(v_c\) のグラフを描くと次のようになります。

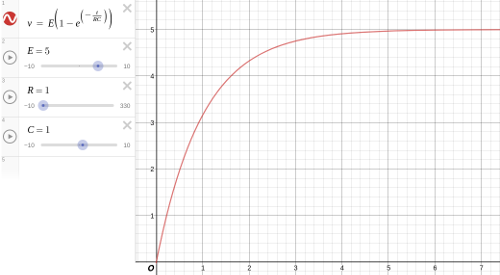
desmos というサイトでこういうグラフが簡単にかけて、パラメータの調整ができたりします。

ここで電源の電圧 \(E = 5\) [V]、抵抗 \(R = 1\) [Ω]、静電容量 \(C = 1\) [F] としてます。

スイッチを押して電源を接続したらスッと電圧が上がって、徐々に \(E\) に近づいていきます。

ちなみに、\(t = R \cdot C \) の時には、上の式で \(t=RC\) として、

\[ \begin{aligned} v_c(RC) &= E \Big( 1- e^{- \frac{RC}{RC}} \Big) \\ &= E ( 1 - \frac{1}{e} ) \\ &\approx E ( 1 - 0.368 ) \\ &= 0.632 \cdot E \end{aligned} \]

となります。つまり \(t=RC\) 時間経ったときに、電源の約 63% の電圧になります。 \(RC\) は時間の単位を持っていて、時定数 といいます。記号は \(\tau\) (タウ) を使うことが多いです。

\(v_c = E\) となるのは、数式の上では \(t\to \infty\) として、

\[ \begin{aligned} \lim_{t \to \infty} E \Big( 1- e^{- \frac{1}{RC} t} \Big) &= E \end{aligned} \]

ということになっていますが、実用上は「無限の時間が経ったらコンデンサが満充電」といわれても困るので、 時定数の 5 倍の時間で満充電 とする場合が多いようです。

具体例

電池の電圧 E = \(1.5\) [V]、抵抗値 \(R = 10\) [kΩ]、静電容量 \(C=100\) [μF] の時には、\(\tau = R \cdot C = 10 \times 10^3 \times 100 \times 10^{-6} = 1\) なので、時定数は 1 秒です。

従って電池を接続して、1 秒後にコンデンサの電圧は \(1.5 \times 0.632 = 0.948\)[V] まで上昇。時定数 \(\tau\) の 5 倍の 5 秒後にコンデンサは満充電ということになります。

以上まとめると、 RC 直列回路では、時定数の 5 倍の時間でコンデンサがフル充電されます。また、その時コンデンサの電圧は上でみた \(v_c(t)\) の式に従って上昇します。